When stability goes belly up

As I noted in my previous post, neoclassical economics made it an item of faith that capitalism was inherently stable, and dismissed arguments to the contrary as no more than left-wing propaganda. My favourite statement of this perspective came from the pen of Nobel Prize winner Ed Prescott, who was one of the key players in introducing the concept of “rational expectations” into economics. Not only was capitalism inherently stable, he claimed in 1999, but it was so stable that we can reliably expect the economy to double the standard of living every 40 years. Marx and his ilk were simply wrong:

“The Marxian view is that capitalistic economies are inherently unstable and that excessive accumulation of capital will lead to increasingly severe economic crises,” Prescott said. “Growth theory, which has proved to be empirically successful, says this is not true. The capitalistic economy is stable, and absent some change in technology or the rules of the economic game, the economy converges to a constant growth path with the standard of living doubling every 40 years.“

About 15 years later, after the dot.com bubble and burst, the subprime bubble and burst, the apparently never-ending ‘Great Recession’ in the US and Europe’s second Great Depression, the alternative argument that capitalism is indeed inherently unstable is looking somewhat better than Prescott’s Panglossian vision.

That’s not to say that instability is always a bad thing: to Schumpeter (and to Austrian economists), instability is an essential part of the creative process of capitalism. Its darker side, which Minsky focused upon, was the tendency for this instability to lead to excessive debt and, ultimately, a Depression.

Though this might surprise some people, I’ve tended to stand closer to Schumpeter than to Minsky on this. Minsky argued that the destructive instability was endemic to capitalism, as much as the creative instability was, because finance necessarily had to be destabilizing. I have tended to argue instead that finance’s destructive tendencies arise because we let the banks finance Ponzi schemes -- bubbles in real estate and shares -- that add to debt without adding to the capacity of society to finance that debt. Eliminate that tendency, I have argued, and the destructive side of finance could be tamed.

Now I’m not so sure—thanks to some modeling I did recently as a prelude to presenting a seminar to staff at the Australian Treasury last week.

This was my second invitation to present to a Treasury audience -- the previous experience was in New Zealand last year. That was a high-level meeting: I had been invited over by the Secretary of the Department, and there was hope that this would lead to a joint project to develop a monetary, Minsky-inspired model for the New Zealand Treasury.

That hope was scuppered by the Treasury economists themselves, who (with some notable exceptions) were hostile to the anything other than neoclassical economic modeling. It didn’t matter a piffle, it seemed, that neoclassical models completely missed the economic crisis of 2007-08, and instead predicted that tranquil economic times lay ahead. Just tweak the models a bit and we can simulate the crisis after it happened, so what’s the problem…

Given that previous experience, I prepared to meet a number spurious objections to my modeling that were thrown up in New Zealand. One in particular was the claim that the instability my models displayed was simply a by-product of the exponential functions I used to simulate the behavior of workers and capitalists. Remove them, I was told, and the instability would disappear.

I knew that was a mathematically false objection: if a model has an unstable equilibrium with exponential functions, it will be unstable with linear ones too. But when you’re arguing with True Believers in a false paradigm, simply telling them that there’s a mathematical theorem that proves them wrong doesn’t cut it: you have to show them (and even that might not work, but it’s worth a try).

So I did something I’ve never done before for my Treasury audience: I rebuilt my Minsky models using strictly linear functions. Though this resulted in unrealistically large cycles when I ran simulations, it also made it much easier for me to do some simple exploration of the properties of my models -- and this led to the surprise I’m leading up to.

My Minsky models themselves are built on the foundation of a model constructed by Richard Goodwin back in the 1960s (Goodwin 1967), and his inspiration came from a verbal model developed precisely one century earlier, by none other than… Karl Marx (Marx 1867, Ch. 25 Section 1). The great appeal of this model to me was that, in a ‘let’s assume we have a can opener’-laden discipline, Goodwin’s model was as close to being assumption-free as you could get.

Starting from the top, to produce output you need factories, and factories can’t produce without hiring workers. The level of employment influences worker’s ability to get wage rises, and profit is basically what’s left after wages have been paid. Capitalists then invest using profits, and that investment determines whether the number of factories increases (because of gross investment) or falls (because of depreciation).

That’s it: if you follow that verbal logic then you understand Goodwin’s model (and even Marx’s prose!). To turn it into a mathematical model, Goodwin assumed the simplest possible relationships between each chain in this causal loop: that each relationship was simply linear. Output was some constant times the amount of capital, workers’ wage demands were some constant times how much the employment rate differed from some threshold level, and so on. Of course, the actual relationships in the real world are very complex and change over time, but this was partly Goodwin’s point (and mine): if even a simple model like this was unstable, then the real world was likely to be more unstable still.

Of course, you might not expect much of interest to come out of such a simple model -- and you’d be wrong. Despite its simplicity, the model generates persistent cycles: its equilibrium is unstable (or technically speaking, neutral) -- and with not an exponential function in sight (see figure 1).

Figure 1: Goodwin's model -- endemic cycles

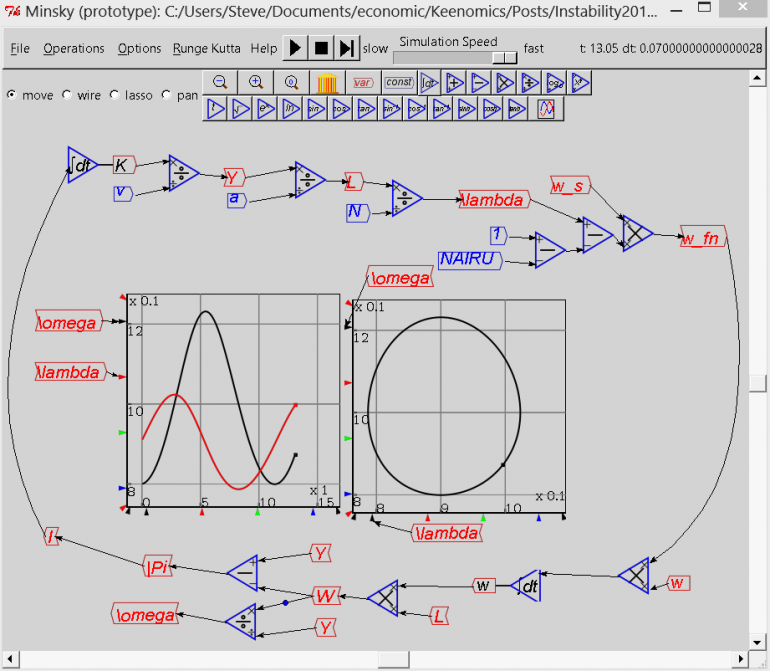
Instead, cycles occur because the wage bill -- the upper-case Wat the bottom of figure 1 -- is equal to the wage rate (w), multiplied by the number of workers employed (L). Multiplying two variables together gives you an inherent nonlinearity, and this is what drives the cycles.

When both wages and employment are rising -- which does happen, as you can see from the left hand plot in figure 1 (during the first three years) -- the product rises even faster, cutting in to profits and reducing investment. This in turn slows down economic growth, which results firstly in falling employment, and then in falling wages as well (from years five to eight in figure 1). This restores profits, leading to more investment, and another cycle: rinse and repeat, without ever approaching equilibrium.

I built my Minsky model by adding a bit of reality. In Goodwin’s simple model, all profits are invested; but in the real world, firms invest less than profits during a slump, but more than profits during a boom -- and bank loans supply the additional revenue for investment in excess of profits, charging interest on the accumulated debt for the service.

This required adding both an investment function -- some relationship between the rate of profit and the level of investment -- and a banking sector. In my published papers I’ve always used an exponential form for the investment-profit relation, but for Treasury -- in case I copped the same neoclassical push-back that I copped in New Zealand last year -- I used a linear one. That led to the model shown in figure 2 (the investment and banking features are added in the lower left hand corner of the diagram).

Lo and behold, chaos -- and without an exponential function in sight. Were I to get the same sort of neoclassical pushback in Canberra that I experienced in Wellington, I had a comeback.

Figure 2: Goodwin plus banks equals ... chaos

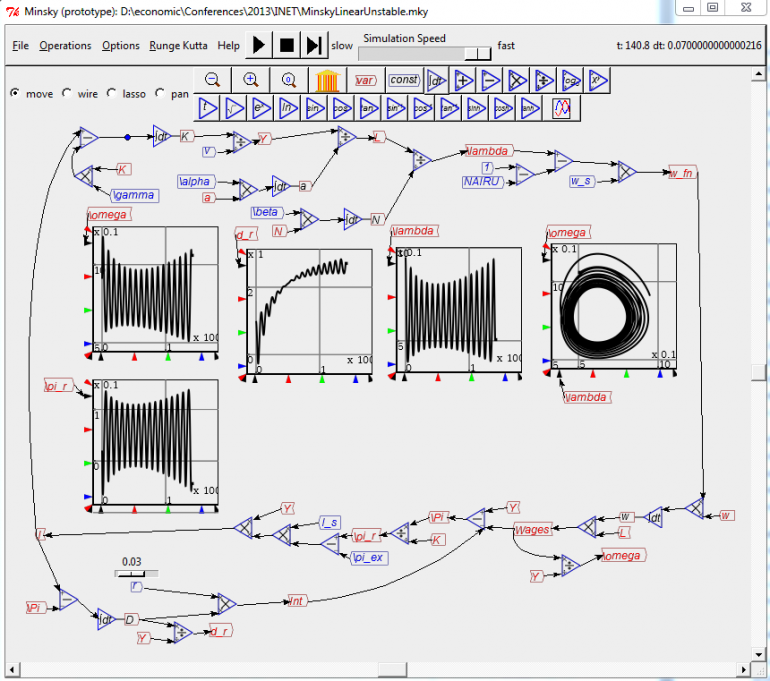
As it happened, I needn’t have worried. I had an attentive and friendly audience in Canberra, and the spurious ‘that only happens because of your exponential functions’ objection didn’t even arise.

But I now had a version of my Minsky model with linear functions, and that made it easy to do something that is very difficult with nonlinear functions: to work out the overall stability of the model.

The simplest metric of stability starts with the model in an equilibrium, pushes it away a tiny fraction, and works out whether it will return to equilibrium or not. If a key value (known by its German name which simply means “inherent value”) is negative, the equilibrium is stable; if it’s positive, the equilibrium is unstable.

This model has two equilibria: a ‘good’ one with positive workers’ share of output, positive employment, and finite debt, and a ‘bad’ one with zero workers’ share, zero employment, and infinite debt -- the economic equivalent of a gravitational Black Hole.

I already knew that the bad equilibrium was unconditionally stable: if you start there, there’s no escape. I expected that the model’s stability around its ‘good equilibrium’ would not be absolute: that there would be some parameter values (rate of interest, response of workers to unemployment, etc.) and some initial conditions (initial debt level, initial employment etc.) for which the equilibrium was stable, and others for which it was unstable.

Here’s where I got my surprise. I was wrong: the ‘good’ equilibrium appears to be unconditionally unstable. If the model starts a small distance away from equilibrium, it will continue to diverge until it ultimately falls into the ‘bad’ equilibrium.

The implication this has for the real world is that perhaps debt crises are, like instability itself, also not an optional extra. Even with nothing other than responsible ‘Schumpterian’ finance, a debt crisis will ultimately occur -- unless we find some mechanism to reduce the level of accumulated debt.

One such method, of course, is inflation -- which isn’t considered in this simple model. Believers in the (inherent stability of the) free market often claim that prices are capitalism’s great leveler: the market mechanism and prices will solve all the problems that capitalism encounters, and the reason critics like me get it wrong is that we don’t consider the price mechanism. I’ll get on to that topic in my next installment on instability.